2.4.5.1. "Memory-Funktion" für ITE *
2.4.5.2. Komplementäre Kanten *
2.4.5.3. Standard-Tripel für ITE *
3.3.4.1. Das File-Menü *
3.3.4.2. Das View-Menü *
3.3.4.3. Das I-T-E-Menü *
3.3.4.4. Verbose-Level-Menü *
3.3.4.5. ?-Menü *
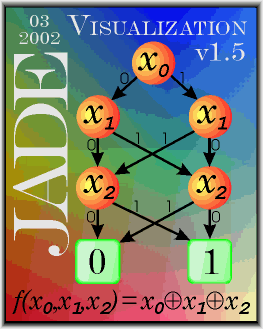
Die Grundidee dieser Arbeit ist, eine grafische Veranschaulichung
beliebiger Boolscher Funktionen in Form spezieller sog. Entscheidungsdiagramme
(engl. decision diagrams) zu realisieren.
Der Benutzer soll in einer einfachen grafischen Oberfläche eine Boolsche Funktion mit allen wichtigen logischen Operatoren (inkl. NOT, AND, OR, NOR, XOR, NAND, …) über einer (fast) beliebigen Variablenmenge eingeben können. Das Programm soll die eingegebene Formel interpretieren (engl. Fachbegriff parsen) und gleichzeitig eine spezielle Datenstruktur (BDD, engl. binary decision diagram) erstellen, welche die eingegebene Funktion eindeutig repräsentiert. Die Eindeutigkeit (Kanonizität) dieser Repräsentation wird dabei eine zentrale Rolle spielen. Das "Synthetisieren" dieser Datenstruktur übernimmt ein spezieller Synthesealgorithmus, genannt "ITE", der sich gerade bei solchen Funktionen anbietet, die durch BDDs repräsentiert werden, wie in dieser Arbeit.
Um die eben geforderte Kanonizität der Repräsentation zu gewährleisten, müssen wir fordern, daß zu jeder fest gewählten Boolschen Funktion genau ein BDD existiert. Dafür brauchen wir zuerst eine feste Ordnung der Variablen in der Funktion, die sogenannte Variablensortierung, damit wir die Reihenfolge der Zerlegung der Funktion festhalten. Wir erhalten ein geordneten BDD, oder kurz OBDD (engl. ordered binary decision diagram). Zusätzlich wird mittels Reduktion aus der verbleibenden Menge äquivalenter OBDDs genau einer zur Repräsentation einer bestimmten Funktion ausgewählt. Daraus ergibt sich dann die geforderte Kanonizität (Beweis siehe [1], Seite 14). Ein derart vollständig reduzierter, geordneter BDD heißt also kurz ROBDD (engl. reduced ordered binary decision diagram). BDDs sind also eine echte Obermenge von ROBDDs.
BDDs sind heute sehr beliebt und können Ansätze für
viele verschiedene Problemstellungen sein. Sie haben sich zu einer Art
"Standarddatenstruktur" entwickelt, sind gut erforscht und lassen sich
einfach handhaben – auch wenn es Anwendungen gibt, für die BDDs zu
eingeschränkt / aufwendig sind.
Die Programmiersprache Java der Firma SUN® zeichnet
sich im Umgang mit speicherintensiven Funktionen als sehr flexibel und
einfach zu bedienen aus (Stichwort "garbage collection"…). Außerdem
ist Java durch seine Ähnlichkeit zu vorhandenen Standard-Programmiersprachen
(wie C++) einfach zu erlernen, und es gibt es eine ganze Reihe vorgefertigter
Grafik- und Hilfsroutinen. Nicht zuletzt verspricht der Einsatz von Java
Plattformunabhängigkeit.
Kapitel 2 wird sich näher mit der theoretischen Grundlage der
Arbeit befassen, sowie wichtige Begriffe klären, die immer wieder
auftauchen werden.
Technischer wird es dann in Kapitel 3. Hier wird auf die Installation und Benutzung des Programms selber eingegangen. Im einzelnen werden die Menüpunkte erklärt und mit Bildschirmfotos erläutert.
Einiges zur programmtechnischen Realisierung (Implementierung) dieser Arbeit in Java wird in Kapitel 4 gegeben.
Auf der CD zur Arbeit befindet sich auch eine Entwickler-Dokumentation, die in allen Einzelheiten die Klassen, Methoden und Variablen der Applikation und seiner Module für den interessierten Programmierer/Weiterentwickler dieser Software erklärt. Diese Dokumentation wurde automatisch generiert mit dem Java-Tool javadoc. Es extrahiert Klasseninformationen und Autorenkommentare und -verweise aus dem Quelltext und erstellt eine komplette HTML-Hilfestruktur. Eine geeignete Übersicht erhält man in der Datei index.html. Voraussetzung zur fehlerfreien Anzeige ist lediglich ein "frame"-fähiger Browser.
Näheres zum Inhalt der CD befindet sich in Kapitel 5.
Theoretische Grundlage der Realisierung ist ein BDD-Package dreier
Amerikaner: Karl S. Brace, Richard L. Rudell und Randal E. Bryant – vorgestellt
1990 auf der 27th ACM/IEEE Design Automation Conference
(vgl. dazu [3]). In ihrem Package entstehen ROBDDs
durch rekursive Aufrufe des sogenannten ITE-Operators. Als Operanden
werden dafür drei fertige ROBDDs (im Weiteren mit F, G und H bezeichnet)
benötigt, welche dann zu einem neuen, größeren ROBDD verschmelzen.
Wichtig bei dieser Art der Synthese ist es, die Kanonizität der so
erzeugten ROBDDs zu gewährleisten.
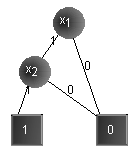
Ein binary decision diagram (BDD) ist ein gerichteter
azyklischer Graph mit genau zwei Senken (=Blätter), die mit 0
und 1 bezeichnet werden und welche die Boolschen Funktionen 0 und
1 repräsentieren. Alle (anderen) Knoten im Graph werden mit einer
Boolschen Variable xi (i ³ 0) bezeichnet; sie bilden die
inneren Knoten. Diese inneren Knoten haben jeweils genau zwei ausgehende
Kanten, die einmal mit 0 ("low"-Kante oder "low"-Sohn)
und einmal mit 1 ("high"-Kante oder "high"-Sohn) bezeichnet
werden. Dabei verweist die ausgehende "low"-Kante auf einen Knoten, der
die entsprechende Boolsche Funktion für xi = 0 repräsentiert,
und die ausgehende "high"-Kante auf einen Knoten, der die entsprechende
Boolsche Funktion für xi = 1 repräsentiert. An jedem
Knoten wird also entschieden, ob die Variable nun 0 oder 1 ist.
Die so gewonnenen Funktionen nennt man auch die Kofaktoren bezüglich
der Variablen xi.
Ein BDD heißt geordnet (OBDD), wenn die Variablen irgendeiner (für dieses BDD festen) Sortierung gehorchen, d.h. auf jedem Weg im gerichteten Graphen ist die Reihenfolge der Variablen der besuchten Knoten identisch mit der Reihenfolge in der vorgegebenen Ordnung (was nicht ausschließt, daß verschiedene Variablensortierungen zum selben OBDD führen können; in der Regel ist dies jedoch nicht der Fall). Die Variablensortierung im Graphen entscheidet über dessen Größe. Das Auffinden der optimalen Variablensortierung ist sehr schwierig. Man kann zeigen, daß das Problem herauszufinden, ob es noch eine bessere Variablensortierung gibt, NP-vollständig ist, d.h. bisher existieren nur Verfahren mit exponentiellem Aufwand. Es gibt aber Heuristiken, die eine effiziente Approximierung liefern. Eine solche Heuristik, das sogenannte Sifting, benutzt auch dieses Package (s. 3.3.3). Der Benutzer des Programms kann die Variablensortierung auch von Hand ändern und so die Auswirkung auf den BDD sofort erfahren.
Ein OBDD heißt reduziert (ROBDD), wenn jeder Knoten im OBDD eine unterschiedliche Boolsche Funktion repräsentiert. Das gilt in erster Linie natürlich auch für den Wurzelknoten des ROBDD, der die komplette Funktion repräsentiert.
Bryant [3] hat als erster gezeigt, daß ein ROBDD wohldefiniert ist. Außerdem wies er nach, daß ein ROBDD eine kanonische Repräsentation einer logischen Funktion darstellt, d.h. zwei Funktionen sind genau dann äquivalent, wenn deren Darstellungen als ROBDD isomorph (also gestaltgleich) sind.
Die Funktion F, die ein Knoten mit Variable xi
repräsentiert, kann man also schreiben als
,
wobei 
die Funktion
mit xi = 1 (also den "high"-Sohn) und 
die
Funktion mit xi = 0 (also den "low"-Sohn) repräsentiert.
Diese Art der "Zerlegung" einer Funktion nach einer Variable nennt man
"Shannon"-Zerlegung oder -Dekomposition. Im BDD ist jeder Knoten
nach Shannon zerlegt.
Um den OBDD in einen ROBDD zu überführen und anschließend
eine kanonische Repräsentation der Ausgangsfunktion zu erhalten, muß
man verschiedene Reduzierungen am Graphen durchführen. Es hat sich
gezeigt, daß zwei Reduktionstypen ausreichen, um die gewünschte
Form zu erhalten. Ein OBDD heißt reduziert (ROBDD),
wenn keine der unten angegebenen Reduktionstypen mehr angewendet werden
können (erst dann ist gewährleistet, daß jeder Knoten eine
unterschiedliche Funktion repräsentiert):
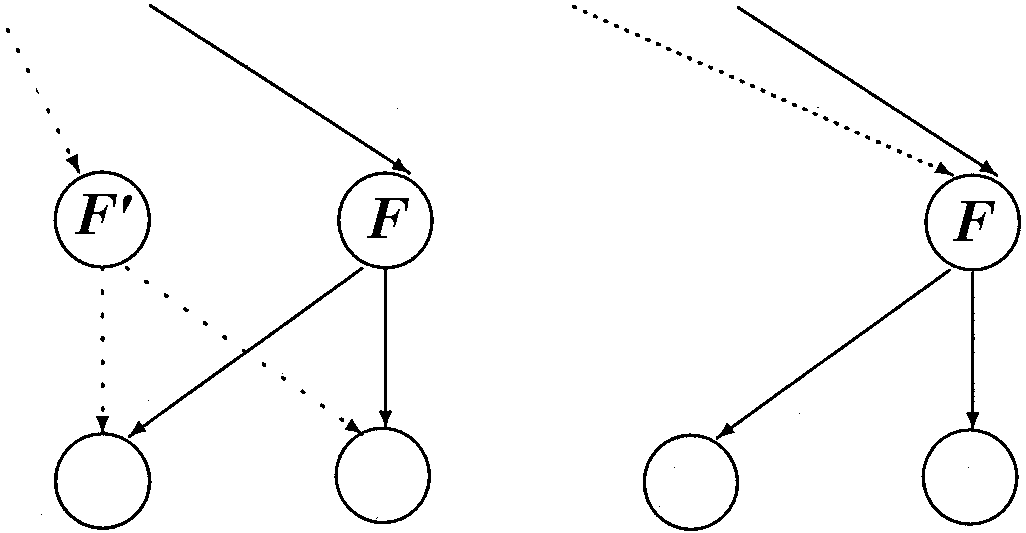
Typ I: "Isomorphie"
Lösche einen Knoten 
und seine ausgehenden Kanten, wenn gilt: Es gibt einen anderen Knoten 
mit 
, der nach derselben
Variable zerlegt ist und hat
denselben low- und high-Sohn wie .
Die eingehenden Kanten von
werden auf umgelenkt.
Ein grafische Veranschaulichung gibt es in Abb 2:
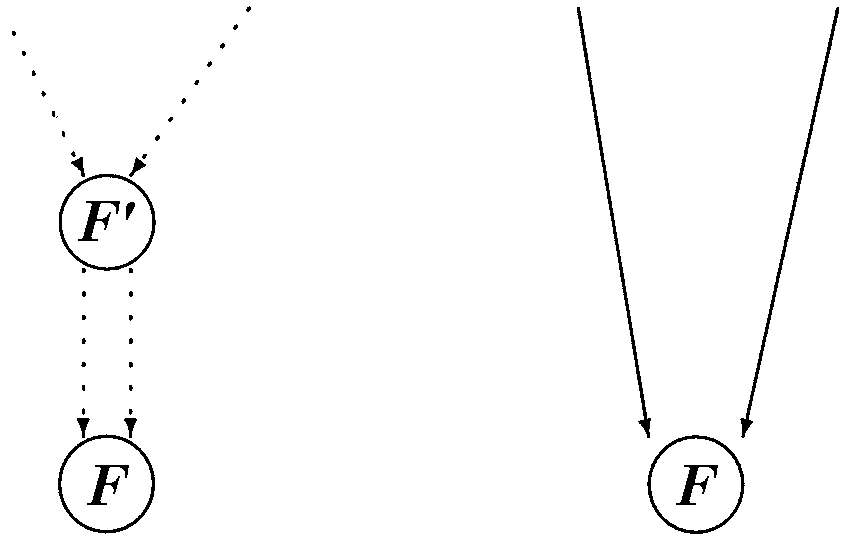
Typ S: "Shannon"
Lösche einen Knoten ,
falls low- und high-Sohn des Knotens auf denselben Knoten zeigen.
Die eingehenden Kanten von
werden auf umgelenkt.
Ein grafische Veranschaulichung gibt es in Abb 3:
BDDs kommen heute im besonderen Maße beim computergestützten
Schaltkreisentwurf (engl. computer-aided design, kurz CAD) zum Einsatz.
Viele hier auftauchende Probleme lassen sich als Sequenz von Operationen
(z.B. AND, OR, NOT, …) beschreiben, welche auf Boolschen Funktionen ausgeführt
werden. Was man benötigt ist also eine effiziente Möglichkeit,
diese Operationen zu verwirklichen. Genau das ist die Aufgabe eines BDD-Packages.
Auf Effizienz wurde allerdings hier nicht der Schwerpunkt gelegt, denn
vielmehr steht in diesem Projekt die Visualisierung im Vordergrund.
Durch die Kanonizität von ROBDDs kann man auch "leicht" die Äquivalenz zweier Boolscher Funktionen testen. Dazu muß man lediglich die dazugehörigen ROBDDs auf Isomorphie prüfen. ROBDDs können zwar im schlechtesten Fall (engl. worst-case) auch exponentielle Größe in der Anzahl der Variablen haben, doch sie sind für die meisten interessanten Funktionen eher klein.
Ebenfalls ein häufig auftauchendes Problem ist der Test auf Tautologie.
Hier möchte man wissen, ob eine Boolsche Funktion für alle Variablenbelegungen
immer zu 1 (oder zu 0) evaluiert. Das ROBDD der konstanten Funktion 1 (bzw.
0) ist einfach nur ein Blatt mit "1" (bzw. "0") markiert. Bleibt also nur
noch, das ROBDD der zu untersuchenden Funktion zu erstellen und mit "1"
(bzw. "0") zu vergleichen.
- Die Blätter im ROBDD bezeichne ich mit 0 und 1.
- Knoten werden mit Großbuchstaben bezeichnet und sind durch das Tripel F=(xi,G,H) eindeutig bestimmt, wobei xi die Boolsche Variable des Knotens F ist und G die Knotenbezeichnung des "high"-Sohnes (auch "then"-Zweig) und H die des "low"-Sohnes (auch "else"-Zweig) darstellt. Das wird auch später in der Implementierung bei der Wahl der Variablennamen so beibehalten (Java ist "case-sensitive", d.h. es unterscheidet zwischen groß- und kleingeschriebenen Variablenbezeichnern)
- Die Topvariable eines Knotens (bzw. BDDs) F ist die Variable, nach der F zerlegt wurde (also die des Wurzelknotens des BDDs F).
- Die Topvariable einer Menge von Knoten ist das Minimum der Topvariablen der einzelnen Knoten, formaler:
, wobei bei der Bildung des Minimums die Variablensortierung berücksichtigt werden muß!
Der ITE-Operator (engl. If-Then-Else)
bildet das Kernstück des BDD-Packages. ITE benötigt drei
Operanden und berechnet die Boolsche Funktion
Wenn F eine Entscheidungsvariable ist, entspricht diese Form genau der Shannon-Dekomposition. Wie man leicht nachvollzieht, kann man mit ITE mindestens alle zweistelligen Boolschen Funktionen berechnen. Eine vollständige Liste gibt es in Abb 4:
Abb 4: Mit dem ITE-Operator
kann man alle
zweistelligen Boolschen Funktionen darstellen
Beispielhaft soll hier der "Beweis" für 
(Nr. 0001) geführt werden:
þ
Die Tatsache, daß man alle zweistelligen Boolschen Funktionen durch verschiedene Aufrufe des ITE-Operators schreiben kann, vereinfacht die Implementation enorm, wie folgender Auszug aus dem Quelltext zeigt (Abb 5: AND-, OR- und NOT-Synthese von Knoten):
[…]
/** Realisierung der AND Funktion
mittels einem ITE-Aufruf
* @param a,b Funktionen,
welche verschmolzen werden sollen
* @return Den so gewonnenen
neuen Knoten (=a*b) */
public node AND(node a, node b) { return ITE(a, b, ZERO); }
/** Realisierung der OR Funktion
mittels einem ITE-Aufruf
* @param a,b Funktionen,
welche verschmolzen werden sollen
* @return Den so gewonnenen
neuen Knoten (=a+b) */
public node OR(node a, node b) { return ITE(a,ONE,b); }
/** Realisierung der NOT Funktion
mittels einem ITE-Aufruf
* @param a Funktion, welche
negiert werden soll
* @return Den so gewonnenen
neuen Knoten (=~a) */
public node NOT(node a) { return ITE(a,ZERO,ONE); }
Abb 5: Auszug aus der Synthese-Klasse.
Mit diesen einfachen Methoden werden die wichtigsten Knotensynthesen bewältigt.
Wir wissen also jetzt, wie man einzelne Funktionen mittels eines Aufrufs des ITE-Operators schreiben kann – gegeben dessen Argumente sind schon in der passenden "ROBDD" Datenstruktur. Doch wie bekommt man die?
Dieses Problem löst eine rekursive Formulierung des ITE-Algorithmus:
Sei Z = ITE(F, G, H) und v die Topvariable von {F, G, H}.
Dann läßt sich Z schreiben als:
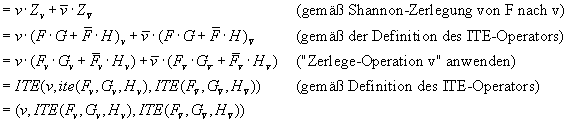
Die Terminalfälle des Algorithmus sind: 
Jeder Knoten Z speichert also ein Tripel mit einer Variablen v, nach der er zerlegt ist und zwei Söhnen, die sich rekursiv aus einem ITE-Aufruf der Kofaktoren ergeben.
Es bleibt also nur noch die Bestimmung der Kofaktoren von F, G und H nach v. Das ist aber hier denkbar einfach, denn es gilt:
Sei F ein Knoten mit F = (w,T,E) und v eine Variable mit v £ w.
Dann gilt:
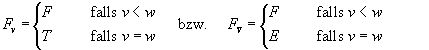
Wobei v < w bedeutet, daß die Variable v gar
nicht in F vorkommt, denn v ist schließlich die Topvariable
von F.
Mit einer Hashtabelle, genannt unique-table, gelingt es,
eine streng kanonische Form im ROBDD aufrecht zu erhalten. Dabei wird jedem
Tripel (v,G,H) ein Knoten im ROBDD zugeordnet. Jeder Knoten im ROBDD
hat also einen entsprechenden Eintrag in der Hashtabelle. Bevor man nun
einen neuen Knoten F = (v,G,H) in das ROBDD einfügt, prüft
man zuerst, ob nicht schon ein entsprechender Eintrag in der Hashtabelle
vorhanden ist. Falls dem so ist, wird der bereits vorhandene Knoten benutzt,
falls nicht wird er eingefügt und ein Eintrag in der Hashtabelle unique-table
wird vorgenommen. Wenn wir induktiv davon ausgehen, daß G
und H schon in der gewünschten kanonischen Form sind, existiert
die Funktion F im ROBDD genau dann, wenn es schon einen Eintrag
für das Tripel (v,G,H) in der unique-table gibt. Nach
Definition erhalten wir somit einen kanonische Repräsentation.
Die Hashtabelle unique-table sorgt also dafür, daß Isomorphien in unserem Graphen gar nicht erst auftreten können. Um die zweite und letzte Reduzierungsart (Typ Shannon) zu bewältigen, bauen wir einen Kofaktor-Test in den ITE-Algorithmus mit ein, welche die Söhne des neu entstehenden Knotens vergleicht. Im Quelltext sieht das (auszugsweise) dann so aus (Abb 6) :
[…]
node fv0 = cofactor0(v,F); //
Kofaktoren berechnen
node fv1 = cofactor1(v,F);
node gv0 = cofactor0(v,G);
node gv1 = cofactor1(v,G);
node hv0 = cofactor0(v,H);
node hv1 = cofactor1(v,H);
node C0 = ITE(fv0, gv0, hv0);
node C1 = ITE(fv1, gv1, hv1);
// Shannon-Reduktion testen
mit Kofaktorvergleich
if (C0.equals(C1)) {
System.out.println("ITE: Shannon-Reduzierung!");
return C1;
}
Abb
6: Auszug aus der Implementation des ITE-Algorithmus. Mit dem Kofaktortest
bewältige ich die Shannon-Reduzierung.
Der komplette ITE-Algorithmus sieht in Kurzform im Pseudocode
folgendermaßen aus (Abb 7):
ite(F,G,H) {
if (Terminalfall) {
return result;
} else {
v = Topvariable(F,G,H);
T = ite(Fv,Gv,Hv);
E = ite(Fv,Gv,Hv);
if (T == E) return T; //
Shannon-Test
R = find_or_add_unique_table(v,T,E);
// Isomorphie
insert_computed_table({F,G,H},R);
return R;
}
}
Abb
7: Der ITE-Algorithmus im Pseudocode.
Die Erweiterung mit computed-table
ist optional; sie wird in Abschnitt 2.4.5.1 näher erklärt.
Hier ein Beispiel, um die Funktionsweise des ITE-Algorithmus zu verdeutlichen (vgl. Abb 8).
Abb 8: Beispiel zum ITE-Algorithmus: I
wird synthetisiert durch iterierten Aufruf von ITE.
Es gibt eine Reihe von Erweiterungen, die zu diesem Thema noch denkbar wären. Als Beispiel seihen hier die drei wichtigsten Ideen genannt:
- Eine "Memory-Funktion" für ITE
- Benutzung "komplementärer Kanten"
- Verwendung von "Standard-Tripel" für ITE
Um den Rechen- und damit den Zeitaufwand des ITE-Algorithmus
zu senken, wird – nach einer Idee von R.E. Bryant – eine zweite Hashtabelle
eingeführt, genannt computed-table. Einmal berechnete Ergebnisse
von ITE werden einfach in die Hashtabelle geschrieben, um bei erneutem
Berechnen der Funktion sofort das Ergebnis liefern zu können. Also
eine Art "Cache".
Betrachtet man beispielsweise die ROBDD Knoten G und 
,
so fällt auf, daß sie einander ähneln, bis auf die Tatsache,
daß ihre Senken 0 und 1 gerade vertauscht sind! Das
kann man sich zu Nutze machen, indem man nicht speichert,
sondern vielmehr eine Kante auf G, welche ein zusätzliches
Bit, das sog. complement-bit, gesetzt hat. Dieses Bit gibt also
an, daß die Funktion, in der diese Kante endet, als komplementär
interpretiert werden muß. Insbesondere entfällt dadurch eine
Senke im Graph, also die 0 oder die 1.
Doch jetzt ist wieder Vorsicht geboten, um nicht die Kanonizität zu verletzen. Wenn man sich alle möglichen Fälle genau anschaut, sieht man, daß es vier verschiede Paare gibt, die jeweils äquivalent zueinander sind (vgl. Abb 9)
Abb 9: Komplementäre Kanten. Diese vier Paare sind funktionell äquivalent.
Um nun wieder für Eindeutigkeit zu sorgen muß man sich eine Eigenschaft aussuchen, die jeweils von den 4 Paaren immer genau ein bestimmtes nur erlaubt; z.B. einigt man sich auf folgende Eigenschaft: Die high-Kante (hier mit 1 beschriftet) muß immer regulär (also nicht-komplementär) sein. Das schafft wieder Eindeutigkeit (Kanonizität).
Der Overhead, der bei der Verwaltung von komplementären Kanten bei ITE entsteht, ist vernachlässigbar klein. Außerdem kommt man ohne zusätzlichen Speicher aus, wenn man einen kleinen Trick anwendet und das low-Bit eines jeden Zeigers zur Kodierung des complement-Bits verwendet.
Es gibt Funktionsparameter F1,F2,F3
und G1,G2,G3 von ITE, für die gilt
ITE(F1,F2,F3) = ITE(G1,G2,G3)
…und es gibt mindestens ein i mit Fi ¹ Gi.
Also definiert man sich auf der Menge von drei Funktionen F1,F2,F3 eine Äquivalenzrelation auf Basis der Boolschen Funktion ITE(F1,F2,F3 ). Wir hätten jetzt gerne aus jeder Äquivalenzklasse einen eindeutigen Repräsentanten, um evtl. die Berechnung zu beschleunigen bzw. die Größe der computed-table zu reduzieren und wiederholte Berechnungen zu vermeiden. Dazu wird zunächst eine Substitution der Parameter gemäß folgendem Schema gemacht:
ITE(F,F,G) ð ITE(F,1,G)
ITE(F,G,F) ð ITE(F,G,0)
ITE(F,G,F) ð ITE(F,G,1)
ITE(F,F,G) ð ITE(F,0,G)
wobei F eine Komplement-Kante meint. Also nächstes werden folgende Standard-Tripel als Repräsentanten aus den Äquivalenzklassen genommen:
ITE(F,1,G) ð ITE(G,1,F)
ITE(F,G,0) ð ITE(G,F,0)
ITE(F,G,1) ð ITE(G,F,1)
ITE(F,0,G) ð ITE(G,0,F)
ITE(F,G,G) ð ITE(G,F,F)
Mit diesen Vereinfachungen läßt sich Zeit und Kosten sparen.
Dieses Kapitel beschäftigt sich mit der Installation / Einrichtung der Anwendung und deren Benutzung. Bei der Installation wird unterschieden, ob sie in einer UNIX- oder einer Windowsumgebung durchgeführt wird.
Um die Java-Applikation selbst starten zu können, braucht man (idealerweise) nur das frei verfügbare Java von der Firma SUN® Microsystems installiert zu haben. SUN bietet Java in zwei Versionen an: Für Entwickler das j2sdk (Java 2 Software Developer Kit) und für Benutzer die Runtime-Version JRE. Jedes dieser Pakete ist natürlich für verschiedene Rechnerarchitekturen erhältlich: z.B.Dieses systemunabhängige Konzept macht es möglich, den einmal erzeugten Zwischen-Code (Java Byte-Code) auf einer Vielzahl von verschiedenen Rechnerarchitekturen ausführen zu können – jedoch sollten diese genügend Reserven mitbringen. Daher hier meine Empfehlungen:
- für PCs (für Microsoft 32-Bit Windows Betriebssysteme, kurz Win32, oder Linux)
- für UNIX Workstations (Solaris)
- Rechner mit installiertem JDK 1.2 oder höher (das beinhaltet auch den korrekt gesetzten Klassenpfad und die swing-Bibliotheken). Fragen zur Installation beantwortet die mitgelieferte Onlinehilfe von Java oder das Internet J
- Grafische Benutzeroberfläche mit mind. 256 gleichzeitig darstellbaren Farben (je mehr desto besser, weil dann nicht gerastert werden muß)
- Eine hohe Bildschirmauflösung wird empfohlen, damit man mehrere Fenster der Applikation gleichzeitig und nebeneinander plazieren kann, ohne daß diese sich großflächig überdecken. Sinnvoll sind Auflösungen ab 1024*768 Pixel.
- Für die Applikation sollten nach dem Starten des Betriebssystems noch mind. 20MB Arbeitsspeicher zur Verfügung gestellt werden können, um ein Auslagern der Seiten zu vermeiden. Das garantiert einen flüssigen Programmablauf. Für PCs mit Win32/Linux bedeutet das idealerweise 64MB Arbeitsspeicher, für UNIX Maschinen etwa das Doppelte. Mit weniger sollte es aber auch akzeptabel laufen.
- Beim PC mit i386 kompatiblen Prozessoren der Pentium-Klasse sollten wir eine Mindesttaktrate von 200MHz ansetzen. Ähnliches sollte bei den versch. UNIX Maschinen gelten. [Die Applikation macht von keiner 2D/3D Beschleunigungshardware explizit Gebrauch und benötigt daher viel "CPU-Zeit"]
- Starten Sie Ihre grafische Benutzeroberfläche X und öffnen Sie ein Terminalfenster.
- Wechseln Sie zuerst in das Verzeichnis, in welches Sie das Programmarchiv kopiert / downgeloaded haben.
- Entpacken Sie die Datei in einem Verzeichnis Ihrer Wahl. Die entpackten Dateien werden zur Laufzeit der Applikation benötigt werden (insbesondere die Hauptdatei OBDDApp.jar). Stellen Sie sicher, daß der Benutzer, der das Programm startet, Read- und Write-Rechte auf allen Unterverzeichnissen und Dateien der eben entpackten Applikation hat (es werden Konfigurationsdateien beim Beenden der Applikation gespeichert).
- Das Startskript JADE-Unix benötigt das das Execute-Recht, welches man explizit mit chmod +x JADE-Unix setzen muß.
- Es wurde automatisch ein Unterverzeichnis angelegt, in welches Sie mit cd <VZ—Name> wechseln. Stellen Sie sicher, daß Java korrekt installiert ist, alle Bibliotheken verfügbar sind, die JDK 1.2 Programme sich im aktuellen Suchpfad befinden und die Klassenpfad-Variable richtig gesetzt ist (mit dem Kommando setenv | grep CLASSPATH kann man sich auch den aktuellen Klassenpfad und mit setenv | grep path den aktuellen Suchpfad für Dateien anzeigen lassen).
- Starten Sie dann das Skript JADE-Unix, um das Programm zu laden, oder geben Sie von Hand java -cp OBDDApp.jar OBDDApp ein. Sollten nun Fehlermeldungen über falsche oder nicht vorhandene Zeichensätze / Schriftarten erscheinen können Sie diese normalerweise getrost ignorieren. Das System sollte dann die fehlende Schriftart durch eine passende ersetzen. Nun sollte sich das grafische Frontend der Anwendung aufbauen. Dem Terminalfenster können Sie zur Laufzeit nützliche Programmausgaben und -informationen entnehmen. Diese Ausgaben lassen sich auch durch den Programmstartparameter -o <file> in eine Datei umleiten. Beachten Sie die Lücke nach dem Schalter –o.
- Sie haben es geschafft! Lesen Sie weiter im Abschnitt über die Bedienung des Programms, um eine kurze Einführung zu erhalten.
- Starten Sie Windows 95/98/2000/NT und öffnen Sie ein DOS-Fenster.
- Wechseln Sie in das Verzeichnis, in welches Sie das Programmarchiv kopiert / downgeloaded haben.
- Entpacken Sie das Archiv mit einem passenden Packer in ein beliebiges Verzeichnis (z.B. der Packer WinZip®). Jetzt entpacken sich eine paar Dateien, welche zur Laufzeit der Applikation benötigt werden (insbesondere die Hauptdatei OBDDApp.jar). Stellen Sie insbesondere unter WindowsNT/2000 sicher, daß der Benutzer, der das Programm startet, Lese-, Schreib- und Execute-Rechte in allen Unterverzeichnissen der eben entpackten Applikation hat (es werden Konfigurationsdateien beim Beenden der Applikation gespeichert).
- Es wurde automatisch ein Unterverzeichnis angelegt, in welches Sie mit cd <VZ-Name> wechseln. Stellen Sie sicher, daß Java korrekt installiert ist, alle Bibliotheken verfügbar sind, die Java executables (v.a. java und javac) sich im aktuellen Suchpfad befinden und die Klassenpfad-Variable richtig gesetzt ist (mit dem Kommando echo %CLASSPATH% kann man sich auch den aktuellen Klassenpfad bzw. mit echo %PATH% den aktuellen Suchpfad anzeigen lassen).
- Starten Sie dann die Batchdatei JADE-Win32, um das Programm zu starten, oder geben Sie von Hand java –cp OBDDApp.jar OBDDApp in der DOS-Box ein. Sollten nun Fehlermeldungen über falsche oder nicht vorhandene Zeichensätze / Schriftarten erscheinen können Sie diese normalerweise getrost ignorieren. Das System sollte dann die fehlende Schriftart durch eine passende ersetzen. Nun sollte sich das grafische Frontend der Anwendung aufbauen. Dem Terminalfenster können Sie zur Laufzeit nützliche Programmausgaben und -informationen entnehmen. Diese Ausgaben lassen sich auch durch den Programmstartparameter -o <file> in eine Datei umleiten. Beachten Sie die Lücke nach dem Schalter –o.
- Sie haben es geschafft! Lesen Sie weiter im Abschnitt über die Bedienung des Programms, um eine kurze Einführung zu erhalten.
Das grafische Frontend von JADE
ist schlicht und einfach gehalten, so daß eine intuitive Bedienung
von Anfang an möglich ist. Trotzdem gehe ich kurz auf die einzelnen
Elemente der Anwendung ein.
Das Hauptfenster besteht aus einer Menüzeile, Statuszeile, Kontrollbuttons, dem Zeichenfenster und Kontrollen zum Strecken der Zeichnung.
Über die Kontrollbuttons (vgl. 3.3.2) kann man zu der Formel in der Eingabezeile (vgl. 3.3.1) ein äquivalentes ROBDD erstellen lassen. Dieser wird dann im schwarzen Zeichenfenster angezeigt. Ist der Step-Mode (vgl. 3.3.4.6) eingeschaltet, kann man die schrittweise Entstehung des ROBDDs verfolgen.
Ist das ROBDD fertig aufgebaut (erkennbar an der Meldung "Waiting
for Input" in der Statuszeile) kann man z.B. einen Knoten im Baum mit einem
Klick auf die linke Maustaste markieren. Die ausgehenden Kanten zu den
Söhnen dieses Knotens werden dann dicker dargestellt, um Mißverständnissen,
die durch das Zeichnen bedingt sind, vorzubeugen.
Ist der markierte Knoten nicht die Wurzel (oberster Knoten) des
ROBDD-Graphen, dann kann man mit dem Pfeil nach oben (rechts neben "Lock
X/Y") die Variablensortierung derart verändern, daß die markierte
Variable mit ihrem Vorgänger in der globalen Variablensortierung getauscht
wird. Daraufhin wird sofort ein neues ROBDD erstellt, welches die Veränderung
visualisiert. Hat man einen Knoten markiert, von dessen beiden Söhnen
höchstens einer ein Blatt (=Terminalknoten, ="0"- oder "1"-markierter
Knoten) ist, dann kann man entsprechend durch Anklicken auf den Pfeil nach
unten (links neben dem "Quit"-Knopf) ein Vertauschen mit dem Nachfolger
in der globalen Variablensortierung erzielen. Dieser Effekt wird ebenfalls
sofort sichtbar.
Durch ein Klicken-und-Ziehen (engl. drag) auf den schwarzen Zeichenbereich kann man den Graphen verschieben.
Mittels der Schieberegler für Zoom-X und Zoom-Y kann man einen
horizontalen bzw. vertikalen Streckfaktor festlegen, der für alle
schwarze Zeichenbereiche (also auch für die Fenster aus 3.3.4.6) gilt.
Die Zeichnung wird dann sofort gestreckt/gestaucht. Ist zusätzlich
noch das Optionsfeld Lock-X/Y aktiviert (Häkchen sichtbar) dann verändert
sich der vertikale und horizontale Streckfaktor in gleichen Teilen, was
zur Folge hat, daß die Zeichnung ge-"zoom"-t wird.
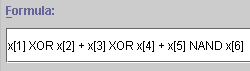
In dieser Eingabezeile kann man eine Boolsche Funktion eingeben.
Bei der Formeleingabe muß folgendes beachtet werden:
- Variablen schreibt man mit einem kleinen x gefolgt von einem Paar eckiger Klammern, [ und ], zwischen denen ein Index i ist.
- Die Konstante Funktion ¦ (x) º 0 heißt "0"
- Die Konstante Funktion ¦ (x) º 1 heißt "1"
- Anwenden muß man diese Operatoren in Infix-Notation, also z.B.
x[1]+x[2] XNOR x[5] ~(x[7] NOR x[9]).- Eine beliebige Klammerung mit runden Klammern, ( und ), ist ebenfalls möglich.
- Bitte beachten Sie, daß - ohne explizite Klammerung einzelner Ausdrücke - folgende Bindungsstärken gelten:
schwach: +, <, >, <=, >=
stärker: *, NAND
stark: XOR, XNOR, NOR
am stärksten: NOT
Hinter den Kontrollbuttons verstecken sich folgende Funktionen (s.
Abb 12):
Um die Variablensortierung im Programm zu ändern, muß
ein kleines Hilfsfenster aufgerufen werden. Es befindet sich im "View"-Menü
unter dem Punkt "Modify variable order…". Hier hat man die Kontrolle
über die Variablensortierung des BDDs (s. Abb 13):
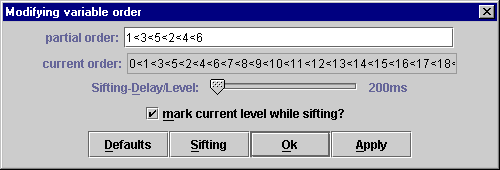
Abb 13: Hilfsfenster zum Einstellen der Variablensortierung im BDD
Bei "partial order:" kann man (wie in der Abbildung zu erkennen)
Teilordnungen definieren, die für die globale Variablensortierung
im BDD gelten sollen. Das ermöglicht ein schnelles und effizientes
Eingeben der gewünschten Sortierung. Wichtig dabei ist nur, daß
man das "<"-Zeichen benutzt. Eine Benutzung
von ">" ist nicht vorgesehen, um Mißverständnisse
zu vermeiden. Leerstellen werden bei der Eingabe nicht berücksichtigt.
Diese partielle Ordnung wird dann über den Schaltknopf "Apply" in die globale Variablensortierung (in Abb 13: "current order") integriert, und der BDD (sofern schon angezeigt) wird ggf. sofort entsprechend angepaßt bzw. neu erstellt.
Die "current order" gibt einen Gesamtüberblick über die momentan vorherrschende globale Variablensortierung im Programm. Dabei werden auch Variablenindizes angezeigt, die evtl. im aktuellen BDD gar nicht verwendet werden.
Ein Häkchen vor "mark current level while sifting" legt
fest, ob bei der Durchführung des Sifting-Algorithmus der momentan
betrachtete Variablen-Level optisch hervorgehoben werden soll (zur Veranschaulichung
der Funktionsweise), oder nicht.
Falls ja, entscheidet der Regler "Sifting-Delay/Level" darüber,
wie lange zwischen zwei Schritten gewartet werden soll (~ Geschwindigkeit
der Animation).
Der Knopf "Defaults" sorgt dafür, daß die Standardvariablensortierung
(aufsteigend) wiederhergestellt wird.
Der Knopf "Ok" schließt das Fenster einfach wieder, ohne
zusätzliche Veränderungen an der Variablensortierung vorzunehmen.
Der Knopf "Sifting" führt am aktuell angezeigten BDD den Sifting-Algorithmus durch. Dabei wird die Variablensortierung des BDDs nach einer bestimmten Heuristik so verändert, daß sich die Anzahl der Knoten im BDD reduziert. Die so gefundene Variablensortierung wird nach Abschluß des Algorithmus in die globale Variablensortierung übernommen und der BDD entsprechend angepaßt / neu erstellt. Beachten Sie, daß während dem Sifting der "Step-Modus" nicht verfügbar ist, selbst wenn er aktiviert wurde. Das kommt daher, daß beim Sifting der komplette BDD exponentiell-in-der-Anzahl-der-Variablen oft neu erstellt werden muß. Normalerweise ist das beim "echten" Sifting nicht notwendig (dort genügt pro Variablentausch ein "Umhängen" der betroffenen Söhne in O(1) ).
In diesem Abschnitt gibt es einen kleinen Überblick, was sich
alles hinter den einzelnen Menüs und deren Unterpunkten verbirgt.
- Save configuration on exit: Beim Verlassen des Programms, werden alle Benutzereinstellungen in einer Datei gespeichert, um eine erneute Eingabe beim nächsten Programmstart zu ersparen. Diese Einstellungen sind z.B.:
> Alle Einstellungen aus den Menüs (sichtbare Fenster und an-/abgewählte Optionen),
> Fensterpositionen,
> Variablensortierung,
> letzte Formel in der Eingabezeile, …
Befindet sich ein Häkchen vor dem Menüpunkt, dann werden diese Einstellungen beim ordnungsgemäßen Beenden (s. nächsten Menüpunkt) des Programms gespeichert. Der Dateiname, der zum Speichern benutzt wird, ist - sofern nicht anders angegeben - entweder der Defaultdateiname (OBDDApp.conf) oder der Dateiname, der als Parameter beim Programmstart mit der Option –c <filename> angegeben worden ist (für eine Übersicht über die versch. Programmparameter vgl. 3.4). Beachten Sie, daß beim Programmstart das ROBDD aus der Formeln in der Eingabezeile nicht automatisch wieder aufgebaut wird.- Exit: Führt zum sofortigen Beenden des Programms ohne erneute Nachfrage.
Die aktuellen Einstellungen werden für den nächsten Programmstart gespeichert, falls gewünscht (vgl. dazu obigen Menüpunkt).
Das View-Menü stellt mehrere Visualisierungsoptionen sowie eine Reihe von Möglichkeiten zur Manipulation der Variablensortierung im BDD zur Verfügung. Im einzelnen sind dies folgende Menüpunkte:
- Swap high/low-edges: Ist diese Option eingeschaltet, dann wird in allen Fenstern bei der BDD-Anzeige die Lage von den ausgehenden low- und high-Kanten an jedem Knoten vertauscht.
Grafisch bedeutet das eine "Achsenspiegelung" am Wurzelknoten des jeweiligen BDDs.- Label edges: Eingeschaltet bewirkt diese Einstellmöglichkeit eine Bezeichnung aller Kanten im BDD mit "0" oder mit "1". "0" bedeutet hierbei, daß es sich um eine low-Kante im Graphen handelt, und bei "1" entsprechend um eine high-Kante.
Ist die Option deaktiviert, da werden die beiden Kantentypen zur Unterscheidung verschiedenfarbig dargestellt (vgl. dazu die Legende in der Grafikanzeige für die Bedeutung der unterschiedlichen Farben).- Label nodes: Geht es in der Darstellung des BDDs lediglich um dessen Gestalt, nicht aber um die Namen der einzelnen Knoten im Graph, dann macht diese Option Sinn. Ist sie aktiv, werden alle Knoten anonym (namenlos) und sind nicht mehr zu unterscheiden. Meistens ist möchte man aber wissen, wie die einzelnen Knoten heißen!
- Invert variable order: Möchte man mal auf die Schnelle die Auswirkungen auf den BDD bei umgekehrter Variablensortierung erkunden, dann bietet sich diese Möglichkeit an. Die Auswirkungen werden grafisch sofort sichtbar, wenn bereits ein BDD im Hauptfenster dargestellt wird.
- Modify variable order…: Hinter diesem Menüpunkt verbirgt sich ein kleines Fenster, in welchem man Kontrolle über die Variablensortierung des BDDs erlangt.
(Vergleiche dazu Abschnitt 3.3.3)- Grid-Layer 1: Mit Aktivierung dieses Menüpunkts werden horizontale Hilfslinien auf dem Graphenhintergrund gezeichnet, um die verschiedenen Level im BDD optisch besser trennen zu können. Zusätzlich zum Ebene-1-Grid gibt es noch das…
- Grid-Layer 2: Dieser Punkt erlaubt eine noch feinere Hilfslinienauflösung. Normalerweise reicht aber das Einblenden der Grid-Ebene 1 bereits für eine gute Übersicht aus. Die Hilfslinien der Ebene 2 sind nur verfügbar, wenn die Ebene 1 bereits aktiviert wurde.
- StartUp window: Ist diese Einstellung aktiv, dann wird beim nächsten Programmstart ein kleines Fenster mit Logo angezeigt. Das Fenster ist nur zur Information und hat sonst keine weitere Funktionalität im Programm.
Das Programm bietet die Möglichkeit, bei der Synthese des fertigen ROBDD zuzuschauen. Genauer bedeutet das, daß sämtliche Aufrufe des ITE-Algorithmus zur Erzeugung des BDDs einzeln mitverfolgt werden können durch sogenannte Parameterfenster. In diesen Fenstern werden die Argumente sowie das Ergebnis des Algorithmus angezeigt. In diesem sogenannten "Step-Mode" kann man Schritt für Schritt die Entstehung des fertigen ROBDDs beobachten. Die einzelnen I-T-E-Menüpunkte werden hier kurz erklärt:
- F-Parameter window: Bei Anwahl dieses Menüpunktes erscheint/verschwindet ein Fenster, in welchem der erste Parameter während des ITE-Synthesealgorithmus angezeigt werden kann. (vgl. 2.4.2)
- G-Parameter window: Bei Anwahl dieses Menüpunktes erscheint/verschwindet ein Fenster, in welchem der zweite Parameter während des ITE-Synthesealgorithmus angezeigt werden kann. (vgl. 2.4.2)
- H-Parameter window: Bei Anwahl dieses Menüpunktes erscheint/verschwindet ein Fenster, in welchem der dritte Parameter während des ITE-Synthesealgorithmus angezeigt werden kann. (vgl. 2.4.2)
- I-Result window: Bei Anwahl dieses Menüpunktes erscheint/verschwindet ein Fenster, in welchem die Ergebnisse der einzelnen Aufrufe von ITE(F,G,H) während des ITE-Synthesealgorithmus angezeigt werden können. (vgl. 2.4.2)
- Step-Mode: Der besagte "Step-Mode" kann mit dieser Menüoption eingeschaltet werden. Ist der Step-Modus aktiv, so wird nach allen Aufrufen von ITE(F,G,H) eine Pause eingelegt, so daß man die Ergebnisse des Aufrufs in Ruhe verfolgen kann. Auf Mausklick/Tastendruck geht es dann weiter. Vorsicht: die Anzahl der rekursiven ITE-Aufrufe steigt schnell an bei längeren Formeln! Beachten Sie, daß der Step-Mode während dem Sifting unabhängig von dieser Einstellung abgeschaltet bleibt.
Unter dieser Rubrik kann man die "Gesprächigkeit" des Programms
einstellen. Das Programm produziert während seiner Ausführung
ständig Meldungen, die (standardmäßig) auf der Konsole
ausgegeben werden, sofern gewünscht. Eine Einstellung von "0: silent!"
bedeutet, daß nur die notwendigsten Meldungen ausgegeben werden.
Je höher der Level, desto "gesprächiger" und detaillierter werden
die Meldungen. 
Vorsicht: Bei Stufe "4: everything!" wird der Output recht unübersichtlich und groß, v.a. wenn ein komplizierter BDD (evtl. sogar mehrmals, wie beim Sifting!) aufgebaut werden muß!
Hinweis: Statt die Meldungen auf der Konsole auszugeben, kann
das Programm auch mit einem Parameter dazu überredet werden, die Ausgaben
in eine bestimmte Datei zu speichern. Der Parameter lautet –o
<filename>.
Wichtig ist die Lücke zwischen –o
und dem Dateinamen.
Unter diesem kleinen Menü verstecken sich eigentlich keine wichtige Funktionen.
Recht hilfreich ist vielleicht die
Abb 14: Das Hilfefenster für das Eingabe–
format der Boolschen Formel
- Help: formula input: Durch Anwählen dieses Menüpunkts öffnet sich ein kleines Fenster, in dem das Eingabeformat für die Formeln erklärt wird. Unten im Fenster wird auch ein Beispiel angezeigt, das man auch in die Formel-Eingabezeile kopieren kann.
- Last message…: Hier öffnet sich ebenfalls ein kleines Fenster, welches die letzte relevante Information / Fehlermeldung enthält.
- About: Ein Fenster mit Informationen über den Autor,
Copyright und Programmversion/-datum.
Abb 15: Das Aboutfenster
Die Applikation kann auch mit Parametern gestartet werden. Die Parameter und deren Funktionen sind:-c <filename> Ändert das Konfigurationsfile auf <filename>.
Sofern Parameter –n nicht gesetzt ist, wird beim Programmstart
versucht, die Konfigurationsdaten aus der angegebenen Datei
zu lesen. Sofern gewünscht, wird beim Beenden des Programms
die Konfiguration in dieser Datei abgelegt.-o <filename> Ändert das Outputfile auf <filename>.
Jetzt werden alle Meldungen, die normalerweise auf der Konsole
ausgegeben worden wären in eine Datei mit dem angegebenen
Namen gespeichert.-n Verhindert ein Einlesen der Konfigurationsdatei
(dann werden die Programmdefaults benutzt!)Die Parameter können beliebig kombiniert werden. Hier sind einige Anwendungsbeispiele zur Verdeutlichung und Erklärung (auf Win32-Systemen entsprechend JADE-Win32 statt JADE-Unix schreiben):
- Die Applikation soll mit Programmdefaultwerten gestartet werden und nach Beendigung der Applikation wird (per Default) die Konfiguration in die Standarddatei OBDDApp.conf gespeichert:
JADE-Unix –n- Die Applikation soll mit Programmdefaultwerten gestartet werden und nach Beendigung der Applikation wird (per Default) die Konfiguration in die angegebene Datei namens neueEinstellung.conf gespeichert:
JADE-Unix –n –c neueEinstellung.conf- Die Applikation soll mit Einstellungen aus Datei MeineLieblingseinstellung.conf gestartet werden und nach Beendigung der Applikation wird (ggf.) die Konfiguration in die eben diese Datei gespeichert. Außerdem soll die Ausgabe des Programms nicht auf der Konsole, sondern in eine Datei namens Output.txt geschrieben werden.
JADE-Unix –c MeineLieblingseinstellung.conf –o Output.txt
Der frei erhältliche Parser namens CUP, der die Boolsche Formel auf die BDD-Datenstruktur abbildet, stammt von Scott E. Hudson, Graphics Visualization and Usability Center, Georgia Institute of Technology und ist im Internet unter http://www.cs.princeton.edu/~appel/modern/java/JLex/
zu finden. CUP steht für "Constructor of Useful Parsers" . Die Version 0.10 ist in der Lage, LALR Grammatiken in Java-Code auf Basis einfacher Spezifikationsdateien zu erstellen, so daß der Benutzer lediglich die Grammatik in einer kleinen Datei angeben muß. Desweiteren sollte man noch eine Java-Datei namens scanner.java editieren, damit der Parser die Eingaben richtig verarbeiten und interpretieren kann. Hier ein Auszug aus der Spezifikationsdatei:
// JavaCup Spezifikation
zum Parsen von
// "erweiterten Booleschen
Ausdruecken" (EBEs)
import java_cup.runtime.*;
/* Anweisungen fuer den
Parsergenerator, wie er den Scanner benutzen soll */
init with {: scanner.init(OBDDApp.parseFormel);
:};
scan with {: return scanner.next_token();
:};
/* Terminal-Symbole (Tokens,
die der Scanner zurueckliefert) */
terminal OR, AND, NAND,
NOR, XOR, XNOR, NOT, ONE, ZERO, SEMI;
terminal GREATER, GREATEREQUAL,
LESS, LESSEQUAL;
terminal LPAREN, RPAREN;
terminal Integer VAR_IDX;
/* Nicht-Terminal-Symbole
-- fuer die Produktionsregeln */
non terminal node expr;
/* Bindungsstaerken: oben:
wenig...unten:stark */
precedence left OR, LESS,
GREATER, LESSEQUAL, GREATEREQUAL;
precedence left AND,NAND;
precedence left XOR,XNOR,NOR;
precedence left NOT, LPAREN;
/* Die Grammatik-Regeln
(kontextfreie Grammatik) */
expr ::= expr:e1 OR expr:e2
{: RESULT = OBDDApp.my_BDD.OR(e1,e2);
:}
|
expr:e1 AND expr:e2
{: RESULT = OBDDApp.my_BDD.AND(e1,e2);
:}
|
expr:e1 NAND expr:e2
{: RESULT = OBDDApp.my_BDD.NAND(e1,e2);
:}
|
NOT expr:e
{: RESULT = OBDDApp.my_BDD.NOT(e);
:}
|
LPAREN expr:e RPAREN
{: RESULT = e; :}
|
expr:e SEMI
{: if (node.verboselevel>=3)
System.out.println("PARSER: result: "+e);
OBDDApp.my_BDD.setlast_node(e);
:}
;
Der Aufbau der Spezifikationsdatei parser.cup ist leicht
durchschaubar. Interessant ist, daß man hier echten Java-Code einbauen
kann, der während dem Parsen den ROBDD mittels ITE erstellen kann,
was das ganze programmtechnisch wesentlich vereinfacht. Sind alle Einstellungen
perfekt, dann muß man nur noch den Parsergenerator starten und bekommt
als Ausgabe einen fertigen Java-Parser, welcher genau auf die jeweiligen
Bedürfnisse zugeschnitten ist.
Die Knoten (engl. nodes) werden in einer Klasse namens node.java spezifiziert. Der Konstruktor kann einmal mit Söhnen ( => innerer Knoten mit Söhnen G und H) und einmal ohne Söhne (=> Blatt) aufgerufen werden.// erstelle inneren Knoten
public node(int vi, node g, node h) {
G = g;
H = h;
v = vi;
last_x = 0;
last_y = 0;
version = 0;
selected=false;
counted=false;
}// erstelle ein Blatt
public node(int vi) {
G = null;
H = null;
v = vi;
last_x = 0;
last_y = 0;
version = 0;
selected=false;
counted=false;
}In dieser Klasse wird auch eine Zahl von Routinen bereitgestellt, die rekursiv auf der Datenstruktur operieren, z.B.
Außerdem verfügt die Klasse über eine Methode zeichnen(), welche rekursiv die grafische Ausgabe des Baumes veranlaßt. Dem geht eine gründliche, rekursive Strukturanalyse mit der Methode structure_analysis() voraus, welche die Koordinaten der einzelnen Knoten berechnet. Das ist alles andere als trivial, denn es gibt einige Einschränkungen, die beachtet werden müssen: z.B. der Graph sollte optisch ansprechend sein und alle Knoten mit derselben Beschriftung sollten sich auf einem Level befinden (vgl. dazu Problem bei 4.3).
- Zählen der Knoten im Graphen,
- Feststellen, ob eine Variable in dem Graphen vorkommt,
- Zählen der Knoten auf einem bestimmten Niveau …
Bisher sind – trotz intensiver Fehlersuche – folgende Probleme und Einschränkungen bei der Benutzung dieser Applikation bekannt:
- Unter gewissen Umständen (v.a. wenn eine Variablenbezeichner mehrfach in einer Formel auftauchen und die Variablensortierung ungeschickt gewählt wurde) kann es vorkommen, daß die Variablen eines Typs nicht auf demselben Level stehen. Das ist z.B. bei der Formel x[1]*x[3]+x[2]*x[4]+x[2]*x[3] mit der Variablensortierung 3<1<4<2 gut nachvollziehbar. Das Problem der korrekten Darstellung ist aber inhärent schwierig!
- Bei gewissen Window-Managern unter Linux bricht das Programm beim Starten mit einer Fehlermeldung ab, daß die aktuelle Farbtiefe nicht unterstützt wird. Möglicherweise ist dies aber auf eine mangelnde Implementierung der Java-Umgebung zurückzuführen.
Die Verzeichnisstruktur der CD mit Microsoft Joliet Filesystem wurde
wie folgt gewählt:
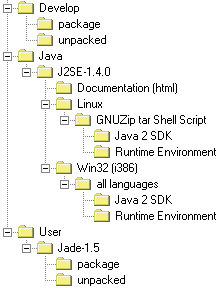
Der Inhalt der CD wurde in drei Bereiche aufgeteilt. Zum einen gibt
es den Teil für den Anwender (Verzeichnis User), der das Programm
lediglich starten möchte; zum anderen gibt es den Teil für den
Entwickler (Verzeichnis Develop), der das Programm neu übersetzen
oder weiterentwickeln will; schliesslich gibt es noch ein separates Verzeichnis
Java in welchem J2SE v1.4.0 enthalten ist (für Windows und
Linux).
Alle Dateien/Verzeichnisse im Verzeichnis Develop sind für Entwickler gedacht. Die folgenden Pfadangaben beziehen sich alle auf dieses Verzeichnis.
- package: enthält ein kompaktes Paket aller relevanten Dateien, die zum Weiterentwickeln bzw. Übersetzen der Applikation notwendig sind.
- unpacked: enthält eine ausgepackte Version des obigen Pakets..
Alle Dateien/Verzeichnisse im Verzeichnis User/JADE-1.5 sind für Endanwender gedacht. Die folgenden Pfadangaben beziehen sich alle auf dieses Verzeichnis. Um JADE benutzen zu können muss mindestens die Runtime Version von Java installiert sein.
- package: Enthält ein Paket von JADE, welches mit j2sdk übersetzt wurde. Dieses kompakte Paket reicht aus, um JADE auf einem Rechner mit installiertem Java ausführen zu können. Für Installationshinweise: siehe Dateien in diesem Verzeichnis.
- unpacked: Enthält eine ausgepackte Version des obigen Pakets zum direkten Starten.
[1] R. Drechsler. Ordered Kronecker Functional Decision Diagrams und ihre Anwendung. Modell Verlag, 1. Auflage, 1996[2] K.S. Brace, R.L. Rudell und R.E. Bryant. Efficient Implementation of a BDD Package. In 27th ACM/IEEE Design Automation Conference, pages 40-45, 1990
[3] R.E. Bryant. Graph - based algorithms for Boolean function manipulation. IEEE Trans. on Comp., 8:677-691, 1986
[4] R. Drechsler und J. Römmler. Implementation and Visualization of a BDD Package in Java. GI/ITG/GMM Workshop "Methoden und Beschreibungssprachen zur Modellierung und Verifikation von Schaltungen und Systemen", Shaker Verlag, S. 219 ff, 2002
Warenzeichen
